Observe a figura.
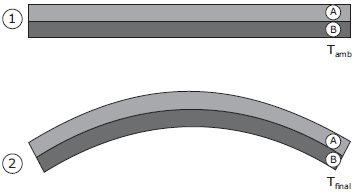
Uma lâmina bimetálica é constituída de duas lâminas de materiais diferentes (A e B na figura acima), unidas firmemente. Em temperatura ambiente, as lâminas são planas e possuem as mesmas dimensões, como na situação 1 da figura. Quando a temperatura delas é modificada, elas se curvam, como na situação 2 da figura. Considerando o coeficiente de dilatação linear dos materiais A e B como sendo A e B, respectivamente, para a situação apresentada, é correto afirmar que
- A) T_{final} > T_{amb},,e,,propto,A < propto B
- B) T_{final} < T_{amb},,e,,propto,A < propto B
- C) T_{final} < T_{amb},,e,,propto,A = propto B
- D) T_{final} > T_{amb},,e,,propto,A = propto B
- E) T_{final} > T_{amb},,e,,propto,A > propto B
Resposta:
A correct answer to this question is E) $T_{final} > T_{amb},$ and $α_A > α_B$.
To explain this answer, let's analyze the situation presented in the figure. We have a bimetallic strip composed of two materials A and B, firmly united. At ambient temperature, the strip is flat and has the same dimensions, as shown in situation 1 of the figure. When the temperature is modified, the strip curves, as shown in situation 2 of the figure.
The key to this problem is understanding the concept of thermal expansion. When the temperature of a material increases, its volume also increases, and it expands. The coefficient of linear thermal expansion (α) is a measure of how much a material expands when its temperature increases. In this case, we have two materials A and B, with coefficients of linear thermal expansion α_A and α_B, respectively.
When the temperature of the bimetallic strip increases, material A expands more than material B, since α_A > α_B. This causes the strip to curve, as shown in situation 2 of the figure. Therefore, we can conclude that the final temperature T_final is greater than the ambient temperature T_amb, and the coefficient of thermal expansion of material A is greater than that of material B.
The other options are incorrect because they do not correctly relate the final temperature and the coefficients of thermal expansion of the two materials. Options A and D imply that the final temperature is less than or equal to the ambient temperature, which is not the case. Option B implies that the coefficients of thermal expansion are equal, which is not true. Option C implies that the coefficient of thermal expansion of material A is less than or equal to that of material B, which is the opposite of what happens.
In conclusion, the correct answer is option E) $T_{final} > T_{amb},$ and $α_A > α_B$. This option correctly relates the final temperature and the coefficients of thermal expansion of the two materials.

Deixe um comentário