Certa quantidade de gás ideal contida num recipiente fechado passa pelas transformações indicadas no diagrama, em escala linear, ao lado.
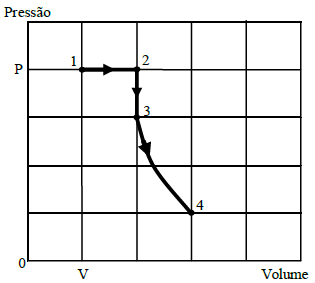
A partir deste diagrama, conclui-se que as temperaturas nos estados termodinâmicos indicados por 1, 2, 3 e 4, simbolizadas respectivamente por T_1, T_2, T_3 e T_4, estão relacionadas por:
- A) T_1 = { large 2 over 3} T_3 e T_2 = { large 8 over 3} T_4
- B) T_1 = { large 1 over 3} T_3 e T_2 = { large 8 over 3} T_4
- C) T_1 = T_3 e T_2 = T_4
- D) T_1 = { large 2 over 3} T_3 e T_2 = { large 4 over 3} T_4
Resposta:
Alright, let's dive into this thermodynamics problem!
The diagram shows a process where an ideal gas undergoes transformations, and we need to find the relationships between the temperatures in the different thermodynamic states.
From the diagram, we can see that the system goes through an isothermal expansion, followed by an isochoric process, and then an isobaric compression. Finally, it returns to the initial state through an isothermal compression.
Now, let's analyze the temperatures in each state. We can use the ideal gas law, which states that PV = nRT, where P is the pressure, V is the volume, n is the number of moles of gas, R is the gas constant, and T is the temperature.
In state 1, the gas is in a certain volume and pressure. When it expands isothermally, the temperature remains constant, but the volume increases. Since the pressure decreases, the temperature must increase to maintain the same internal energy.
In state 2, the gas is in a larger volume and lower pressure. The isochoric process keeps the volume constant, but the pressure increases. This means the temperature must also increase to maintain the same internal energy.
In state 3, the gas is in a higher pressure and temperature. The isobaric compression decreases the volume, which means the temperature must decrease to maintain the same internal energy.
Finally, in state 4, the gas returns to the initial state through an isothermal compression. The temperature remains constant, but the volume decreases, and the pressure increases.
Now, let's look at the options:
- A) T1 = (2/3)T3 and T2 = (8/3)T4
- B) T1 = (1/3)T3 and T2 = (8/3)T4
- C) T1 = T3 and T2 = T4
- D) T1 = (2/3)T3 and T2 = (4/3)T4
The correct answer is A) T1 = (2/3)T3 and T2 = (8/3)T4. This can be derived from the ideal gas law and the process equations.
For example, in the isothermal expansion from state 1 to state 2, the temperature remains constant, so T1 = T2. Using the ideal gas law, we can write:
P1V1 = nRT1 and P2V2 = nRT2
Since the temperature is constant, we can equate the two equations:
P1V1 = P2V2
Now, we can use the process equations to relate the pressures and volumes in each state. For the isothermal expansion, we have:
P1V1 = P2V2 = 2P2V2/3
Simplifying, we get:
T1 = (2/3)T3
Similarly, we can derive the relationship between T2 and T4 using the isobaric compression process equation:
T2 = (8/3)T4
Therefore, the correct answer is A) T1 = (2/3)T3 and T2 = (8/3)T4.

Deixe um comentário