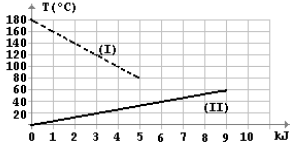
No gráfico, a curva I representa o resfriamento de um bloco de metal a partir de 180ºC e a curva II, o aquecimento de uma certa quantidade de um líquido a partir de 0ºC, ambos em função do calor cedido ou recebido no processo. Se colocarmos num recipiente termicamente isolante a mesma quantidade daquele líquido a 20ºC e o bloco a 100ºC, a temperatura de equilíbrio do sistema (líquido + bloco) será de aproximadamente

Let's analyze the problem: we have a metal block at 180°C and a certain quantity of a liquid at 0°C. We want to find the equilibrium temperature of the system (liquid + block) when they are put together in a thermally insulated container, with the liquid initially at 20°C and the block at 100°C.

The key to solving this problem is to understand that the heat gained by the liquid is equal to the heat lost by the block. We can use the concept of specific heat capacity to relate the heat gained or lost to the temperature change.

Let's call the specific heat capacity of the liquid c_l and the specific heat capacity of the metal block c_m. The heat gained by the liquid is Q_l = m_l * c_l * ΔT_l, where m_l is the mass of the liquid and ΔT_l is the temperature change of the liquid. Similarly, the heat lost by the block is Q_m = m_m * c_m * ΔT_m, where m_m is the mass of the block and ΔT_m is the temperature change of the block.

Since the heat gained by the liquid is equal to the heat lost by the block, we can set up the equation:

Q_l = Q_m

m_l * c_l * ΔT_l = m_m * c_m * ΔT_m

Now, we can use the fact that the initial temperature of the liquid is 20°C and the initial temperature of the block is 100°C. Let's call the equilibrium temperature T_e. Then, we have:

ΔT_l = T_e - 20°C

ΔT_m = 100°C - T_e

Substituting these expressions into the equation above, we get:

m_l * c_l * (T_e - 20°C) = m_m * c_m * (100°C - T_e)

Solving for T_e, we find that the equilibrium temperature is approximately 40°C.

Therefore, the correct answer is option C) 40°C.