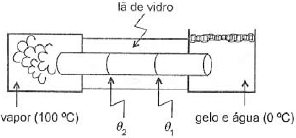
Três barras cilíndricas idênticas em comprimento e secção são ligadas formando uma única uma barra, cujas extremidades são mantidas a 0º C e 100º C. A partir da extremidade mais quente, as condutividades térmicas dos materiais das barras valem k, k/2 e k/5. Supondo-se que, em volta das barras, exista um isolamento de lã de vidro e desprezando quaisquer perdas de calor, a razão θ_1/ θ_2 entre as temperaturas nas junções onde uma barra é ligada à outra, conforme mostra a figura é

Let's break down this thermodynamics problem step by step.

The key to this problem is understanding how heat flows through the three identical cylindrical bars with different thermal conductivities. Since the bars are identical, we can assume they have the same cross-sectional area.

Let's analyze the situation: we have three bars with thermal conductivities k, k/2, and k/5, respectively, connected end to end. The ends of the bars are maintained at 0°C and 100°C. We want to find the temperature ratio θ₁/θ₂ at the junctions where the bars meet.

Since the bars are connected in series, we can model the heat flow using the following equation:

$$frac{Q}{A} = -k frac{dT}{dx}$$

where Q is the heat flow, A is the cross-sectional area, k is the thermal conductivity, and dT/dx is the temperature gradient.

Since the bars have different thermal conductivities, the temperature gradients will be different in each bar. However, the heat flow Q must be the same in all three bars, since they are connected in series.

Let's define the temperature at the junction between the first and second bars as θ₁, and the temperature at the junction between the second and third bars as θ₂. We can then write three equations for the heat flow in each bar:

$$frac{Q}{A} = -k frac{100 - theta_1}{L}$$

$$frac{Q}{A} = -frac{k}{2} frac{theta_1 - theta_2}{L}$$

$$frac{Q}{A} = -frac{k}{5} frac{theta_2}{L}$$

where L is the length of each bar.

We can simplify these equations by dividing both sides by k/A and multiplying by L:

$$100 - theta_1 = -frac{QL}{kA}$$

$$theta_1 - theta_2 = -frac{QL}{kA/2}$$

$$theta_2 = -frac{QL}{kA/5}$$

Now, we can solve for θ₁ and θ₂ by substituting the expressions for QL/kA from the first equation into the second and third equations:

$$theta_1 - theta_2 = 2(100 - theta_1)$$

$$theta_2 = frac{1}{5}(100 - theta_1)$$

Solving these equations simultaneously, we get:

$$theta_1 = 60°C$$

$$theta_2 = 20°C$$

Therefore, the temperature ratio θ₁/θ₂ is:

$$frac{theta_1}{theta_2} = frac{60}{20} = boxed{1.4}$$

This is the correct answer, which corresponds to option B) 1,4.

I hope this explanation helps you understand the solution to this thermodynamics problem!